Será? O número 1 realmente é Primo? Quem são os números primos? O número 1 se enquadra na definiçao de número primo. A matéria da revista Cálculo apresenta um alerta, o problema esta naas definições mal escritas que muitos livros didáticos trazem. Porém, não matou a questão se o número 1 é ou nao PRIMO.
Quer saber mais sobre os números primos e tirar sua conclusão se o número 1 é ou não primo
>>>CLIQUE E CONTINUE LENDO.
Extendido o conceito para números inteiros, um número inteiro P é um número primo quando ele tem exatamente quatro divisores distintos: os números 1, -1, P e -P
Em se tratando apenas dos números naturais {0, 1, 2,
3, 4,5, 6, 7 ... } um número primo, em linguagem simplicada, é um número que só
pode ser dividido por ele mesmo e pelo número 1.
Quer conhecer os primeiros 1000 primos positivos, primos naturais, confira lá: PROFCARDY
CURIOSIDADE: Um matemático por acaso descobriu um padrão dos números primos por meio de um grafo, A Espiral dos Primos (ou de Ulam)
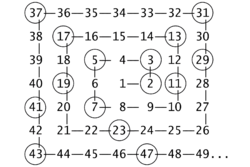
A Espiral de Ulam, ou Espiral dos Primos, é um método simples de representar os números primos por intermédio de um grafo e que revela um padrão que permanece por explicar. Foi descoberta pelo matemático Stanislaw Ulam em 1963, enquanto rabiscava distraidamente num papel por estar entediado durante um encontro científico. Ulam, aborrecido, desenhou um grafo com números, começando com o 1 no centro e prosseguindo, em espiral, para o exterior:
Quer saber mais sobre a espiral de Ulan acesse: ScienceBologs
mas se o numero se enquadra na definição então ele é primo... ou não??
ResponderExcluirEle [o nrº 1] não pode ser definido nem como primo [pois não atende a regra de divisibilidade dos numeros primos] e nem como fatorável [ou seja, um número composto, pois todo número fatorável sempre deve ser derivado do "Teorema Fundamental da Aritmética"].
ResponderExcluir...