Ângulos Notáveis, a música.

Sei que não é natal... mas vai ai uma musiquinha para você recordar dos ângulos notáveis da trigonometria e construir a tabela com seus valores de seno, cosseno e tangente sem maiores complicações.

Um, dois três...Três, dois um!
Tudo sobre dois.
Raiz no três e também raiz no dois

Um, dois três... Três, dois um!
Tudo sobre dois.
Raiz no três e também raiz no dois

A tangente é diferente,
olha só minha gente:
Raiz de três sobre três, um e raiz de três

Quer saber mais sobre de onde vieram esses valores dos ângulos notáveis
>>> Clique e verifique

Os ângulos notáveis

Os ângulos 30°, 45° e 60° são chamados notáveis por aparecerem frequentemente em cálculos. Vamos determinar o seno, cosseno e tangente de cada um deles. Para isso, vamos considerar o triângulo equilátero ABC da figura 1:

[Figura 1]

Podemos destacar algumas relações:
Cada lado do triângulo mede l;
AD é a bissetriz de BÂC;
AD é a mediana de BC, dividindo BC em duas partes iguais de tamanho l/2 em D;
A altura h pode ser escrita em função dos lados l, da seguinte forma:




Determinação do seno, cosseno e tangente de 30° e 60°
O seno de um ângulo é definido como a razão do cateto oposto a este ângulo pela hipotenusa do triângulo:



O cosseno de um ângulo é definido pela razão entre o cateto adjacente a este ângulo pela hipotenusa do triângulo:



A tangente de um ângulo é definida pela razão entre o cateto oposto pelo cateto adjacente a este ângulo:



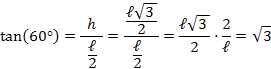
Determinação do seno, cosseno e tangente de 45°
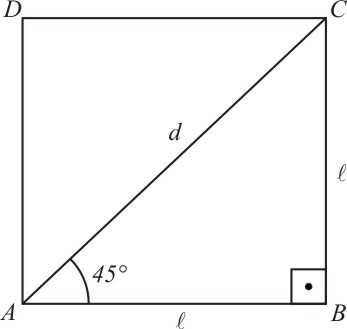
Para calcularmos o seno, cosseno e tangente de 45°, vamos considerar o quadrado mostrado na figura 2:

[Figura 2]

A diagonal d forma com os lados l um ângulo de 45° e podemos escrever a diagonald em função dos lados l:






Vamos, agora, construir uma tabela com os ângulos notáveis: