Equação do 2° Grau e suas aplicações

Equações de 2º grau no nosso cotidiano

 

De volta e meia eu me deparo com uma postagem com a imagem acima no facebook. Praticamente um alerta, um grito sobre o não conhecimento de aplicações da equação do 2° grau e tudo aquilo que está ligado a ela. De fato isto revela uma falha (talvez) sobre o ensino mecânico da matemática e o trabalhar uma técnica desconectado com a realidade ou com situações cotidianas.

Ok. Existem falhas no ensino de matemática, eu como professor assumo em parte essa falha na minha prática docente. Porém preciso destacar que em alguns anos do ensino precisamos treinar bem uma técnica ou um método de cálculo antes, para ficar afiado para as suas aplicações. 

Enfim, para tentar amenizar essa realidade (Passar mais um dia e não usar delta e Bhaskara para nada) e passar a ver as importância e as aplicações da equação do 2° grau foi pesquisado as algumas aplicações desse conhecimento matemático. 

QUER SABER MAIS SOBRE AS APLICAÇÕES DA EQUAÇÃO DO 2°GRAU

>>>>> Clique e continue lendo 

Temos como conceito inicial que uma equação é uma expressão matemática que possui em sua composição incógnitas, coeficientes, expoentes e um sinal de igualdade. As equações são caracterizadas de acordo com o maior expoente de uma das incógnitas, expoente este que determina o grau da equação.

São exemplos de equações com uma variável (x):

3x + 9 = 0, o expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.

2x² + 2x + 6 = 0, temos duas incógnitas x nessa equação, nota em que uma delas possui o maior expoente, determinado por 2. Essa equação é classificada como do 2º grau.

Temos que uma função do 2º grau obedece à seguinte lei de formação f(x) = ax² + bx + c,  onde  a, b e c são os coeficiente e a precisa ser diferente de zero. Além disto, sabemos que a função do segundo grau descreve no gráfico uma parábola e muitos movimentos podem ser escrito por uma parábola.

Equações do 2° grau e suas aplicações

Não se engane, mesmo sem perceber as equações do 2º grau e a função do 2° grau estão presentes em inúmeras situações cotidianas. É claro que nós não a usamos todos os dias ou em tudo. Você não acorda num belo domingo de manhã e tem que ao escovar os dentes resolver um delta ou calcular a raiz da equação para um sorriso perfeito. Mas que as aplicações existem existem.

Como exemplo temos que,

•  Movimento de um projétil - Você já deve ter estado na beira de um rio ou de um lago e atirado uma pedra para o centro da água ou então jogado um objeto ou dado uma bicuda pro alto em uma bola. Note que como será a trajetória desse movimento? Uma parábola, a função do 2° grau que descreve este movimento. Olha uma equação do 2° grau ai gente !!!

 Veja se a trajetória de um projétil, perceba o movimento descrito, uma parábola. A equação do segundo grau é forte presença ai. Por exemplo, para calcular a altura máxima atingida você presisa calcular o delta, para descobrir o ponto de partida e chegada é necessário resolver a equação e achar os valores de x.

 Veja também quando é arremessado uma bola de canhão ou quando atira ao centro do lago se parece com a que aparece nas seguintes simulações, uma parábola.

•    na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo.

Na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão 

S = S₀ + V₀t + (at²)/2, onde  a: aceleração, S: espaço, V: velocidade e t: tempo.

Olhem só:  Um móvel realiza um MUV obedecendo à função S = 2t² - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?  

Olha uma equação do 2° grau ai gente !!!

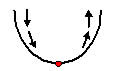
Resolução: A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:

• Olha outra aplicação na física da equação do 2° grau a Lei da Queda dos Corpos 

No estudo de física a queda livre é uma particularização do movimento uniformemente variado (MRUV). Um famoso físico e astrônomo italiano chamado Galileu Galilei, introduziu o método experimental e acreditava que qualquer afirmativa só poderia ser confirmada após a realização de experimentos e a sua comprovação. No seu experimento mais famoso ele, Galileu Galilei, estando na Torre de Pisa, abandonou ao mesmo tempo esferas de mesmo peso e verificou que elas chegavam ao solo no mesmo instante. 

Quando dois corpos quaisquer são abandonados, no vácuo ou no ar com resistência desprezível, da mesma altura, o tempo de queda é o mesmo para ambos, mesmo que eles possuam pesos diferentes.

O movimento de queda livre trata-se de um movimento acelerado, sofre a ação da aceleração da gravidade, aceleração essa que é representada por g e é variável para cada ponto da superfície da Terra. Porém para o estudo de Física, e desprezando a resistência do ar, seu valor é constante e aproximadamente igual a 9,8 m/s2.

As equações matemáticas que determinam o movimento de queda livre são as seguintes:

 nesta fórmula:

 d é a distância percorrida pelo corpo até chegar ao chão;

 G é a constante aceleração da gravidade;

 t é o tempo que o corpo leva para chegar ao chão.

Vc consegue colocar esta fórmula, que calcula a distância em função do tempo da queda, na forma de uma equação do 2º grau? Como seria?

  

 Saiba mais sobre os experimentos de Galileu, clique aqui.

• E nas construções, na engenharia. A matemática é a base se todas as soluções da engenharia. Vc já percebeu o formato de algumas pontes e construções? Será que ela tem relação com a equação do 2° grau ou com uma parábola?

   

A Ponte Juscelino Kubitschek em Brasília também é uma lindíssima ponte que merece ser vista!

Está ponte ao lado (Ponte JK no DF) ao ser projetada os seus arcos arquitetônicos foram descrito através função quadrática ( três arcos logo três parábolas). Será que estes arcos podem ser descritos por meio de uma função do segundo grau?
Olha uma equação do 2° grau ai gente !!!

Se agente pensar um pouquinho mais agente descobre outras aplicações da equação de 2° grau e da função do 2° grau. Agora por favor não passe nem mais um dia sem saber para que e por que estudamos este importante e fundamental tema da matemática. Não tenha a mente pequena, amplie seus horizontes e se abra para novos conhecimentos.

• Equação do 2° grau na Geometria - Dentre os conteúdos inerentes ao 9º ano do Ensino Fundamental, destacaremos cálculos envolvendo áreas e desenvolvimento de equações do 2º grau incompletas. Esses conteúdos podem ser trabalhados visando à fixação de dois importantes conteúdos em um único momento. Assim, envolve a interpretação de problemas, construção geométrica de figuras planas, elaboração e resolução de equações do 2º grau.

Exemplo 1
Um retângulo possui a medida de seu lado maior igual ao quádruplo do lado menor, e área medindo 256 m². Determine a medida de seus lados.

 Informe que, para calcularmos a área de uma região retangular devemos multiplicar o comprimento pela largura. Observe:


O lado de maior comprimento mede 32 metros e o de menor comprimento, 8 metros.

Exemplo 2
Um trapézio possui área medindo 384 cm². Temos que a medida da altura é o dobro da medida da base menor, e que a base maior possui a mesma medida da altura. Determine o comprimento da base maior, base menor e altura desta figura.

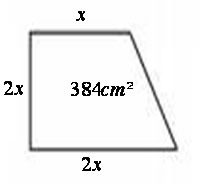
Área do trapézio



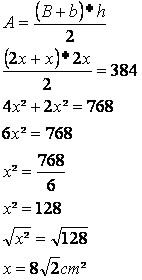
Lado maior: 2 * 8√2 → 16√2 cm
Lado menor: 8√2 cm
Altura: 16√2 cm

  

Fontes Bibliográficas:

Mundo Educação http://www.mundoeducacao.com/fisica/queda-livre.htm
Tecciencias - UFBA http://tecciencia.ufba.br/equacao-do-2o-grau/equacoes-de-2o-grau-no-nosso-cotidiano
Brail Escola http://www.brasilescola.com/matematica/equacao-2-grau.htm
Brasil Escola http://educador.brasilescola.com/estrategias-ensino/relacionando-geometria-equacoes-2-o-grau.htm